Ceramic Capacitor Bank Validation: The Final Power Layer at -70°C

Previous characterization established that the supercapacitor becomes functionally useless below -55°C - its ESR increases 65× and it can no longer deliver meaningful current. The theory behind the cascading power architecture predicted that ceramic capacitors, with their solid dielectric and temperature-stable performance, would seamlessly take over when the supercapacitor fails. This test was designed to validate that handoff.

The experiment used a minimal ceramic bank (408 μF) deliberately undersized relative to final requirements. The goal wasn’t to demonstrate a production-ready system—it was to confirm that ceramics behave predictably at extreme cold and that the supercap-to-ceramic transition occurs as expected. More capacitance will be needed for the final design; this test establishes the baseline.

The test validated the ceramic capacitor behavior as predicted. The supercapacitor failed right on schedule at -55°C, and the ceramics performed exactly as their temperature-stable specifications promised.

The surprise was something we hadn’t anticipated: below -65°C, the battery open-circuit voltage collapses to unusable levels. High internal resistance we can handle—the cascade architecture accumulates energy via trickle charging over time. But voltage collapse below the buck converter’s 2.5V minimum (or the STM32/LoRa’s 1.8V minimum for direct connection) represents a hard floor that no amount of capacitance can overcome.

Battery OCV Collapse

Test Configuration: The Complete Power Stack

Unlike previous characterizations that isolated individual components, this test evaluates the complete power cascade under realistic load conditions:

2S LTO Battery Pack:

Configuration: Two HTC1015 cells in series
Nominal voltage: 4.8V (2.4V per cell)
Capacity: 40 mAh per cell
Pre-test state: Fully charged at room temperature

Supercapacitor:

Type: 5.5V rated EDLC
Capacitance: 1.5 mF (1500 μF)
Configuration: In parallel with 2S LTO battery
Function: Medium-term energy buffer

Ceramic Capacitor Bank:

Type: Class I (C0G/NP0) ceramic capacitors
Total capacitance: 408 μF
Configuration: Bank in parallel with supercapacitor
Voltage rating: 6.3V minimum per capacitor
Function: Final-layer pulse power delivery

Load Profile:

Current: 25 mA constant current load
Duration: 60 ms pulse
Equivalent energy: 25 mA × 5V × 60 ms = 7.5 mJ per pulse
Purpose: Simulates reduced-power LoRaWAN transmission (SF7, minimum packet)

Test Method:

Thermal chamber with controlled ramp from -55°C to -70°C
2-hour thermal soak at each temperature point
No-load voltage measurement (Vmax)
25 mA load for 60 ms, voltage measured at end of pulse (Vmin)
Notes recorded for anomalous behavior

Why 25 mA for 60 ms?

Previous characterizations used 50-100 mA loads to simulate normal LoRaWAN transmission. This test uses a significantly reduced load for critical reasons:

Transmission Power Trade-off:

At extreme cold, the Stratosonde firmware can select a degraded transmission mode:

Normal mode: 50 mA @ 3.3V for 100+ ms (SF10/SF12 for long range)
Degraded mode: 25 mA @ 3.3V for 60 ms (SF7, minimum packet, reduced power)

The reduced current load serves two purposes:

Lower instantaneous current reduces voltage sag from ESR effects
Shorter duration requires less total energy extraction

Buck Converter Considerations:

For 25 mA output at 3.3V = 82.5 mW output power. At 85% efficiency, this requires 97 mW input power. At 5V input: 19.4 mA input current. At 3V input (degraded): 32.4 mA input current.

The 25 mA load applied directly to the capacitor bank slightly exceeds the actual input requirement, providing conservative margin for the characterization.

Results: The Complete Picture

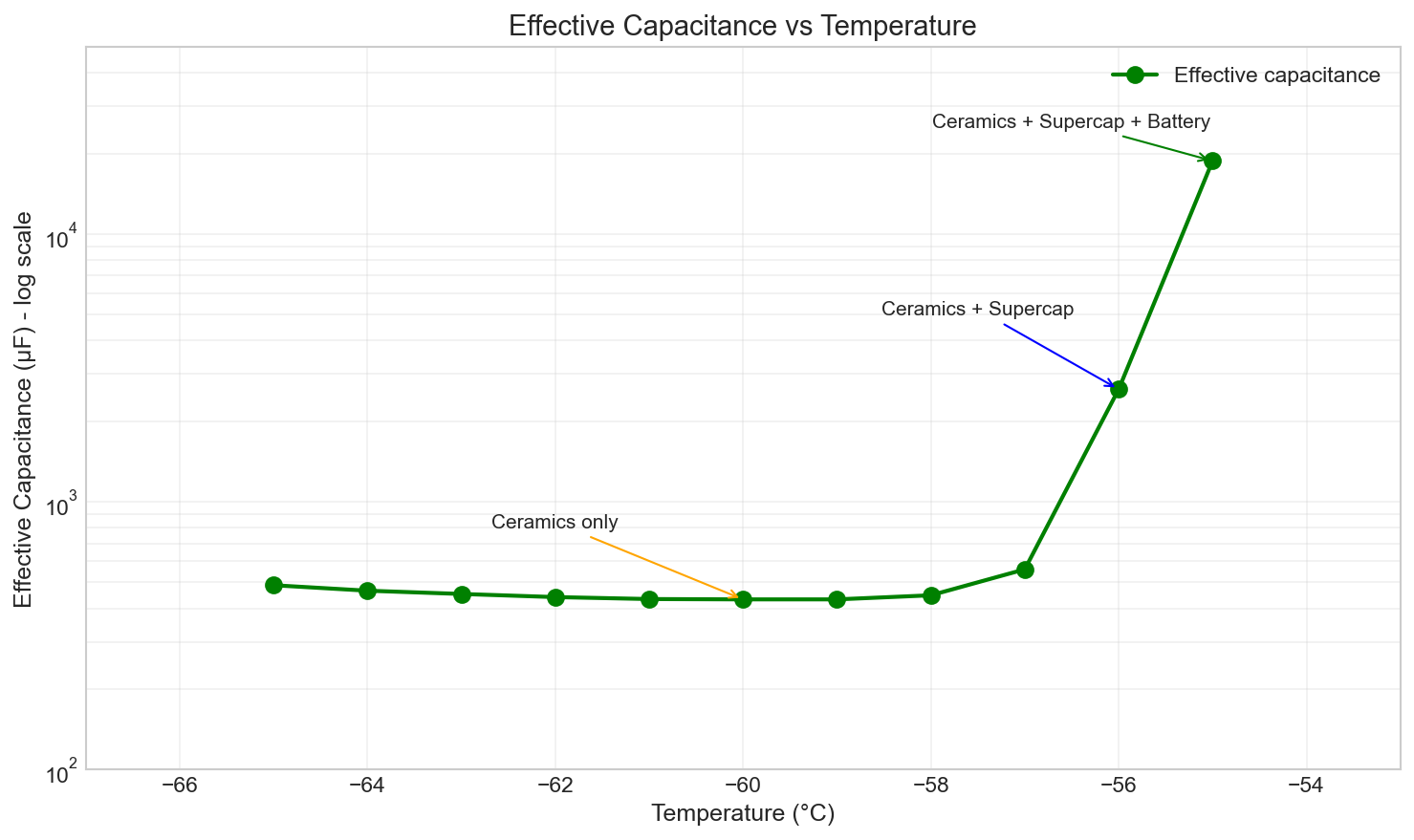
The test data reveals the transition from supercap-dominated operation to ceramic-only operation, and ultimately to battery voltage collapse. The effective capacitance calculation (C = Q/ΔV = 1.5mC/ΔV) reveals which power layer is doing the work at each temperature:

Complete Temperature Response with Effective Capacitance Analysis:

Temp (°C)	Vmax	Vmin (25mA, 60ms)	ΔV	C_effective	Interpretation
-55	5.07 V	4.99 V	80 mV	18.75 mF	Supercap + battery contributing (working)
-56	4.84 V	4.27 V	570 mV	2.63 mF	Supercap degrading but still contributing
-57	4.81 V	2.13 V	2.68 V	560 μF	Supercap failed—ceramics alone
-58	4.80 V	1.45 V	3.35 V	448 μF	Ceramics only (below buck 2.5V min)
-59	4.77 V	1.30 V	3.47 V	432 μF	Ceramics only
-60	4.70 V	1.23 V	3.47 V	432 μF	Ceramics only
-61	4.55 V	1.09 V	3.46 V	434 μF	Ceramics only
-62	4.40 V	0.998 V	3.40 V	441 μF	Ceramics only
-63	4.10 V	0.788 V	3.31 V	453 μF	Ceramics only
-64	3.81 V	0.59 V	3.22 V	466 μF	Ceramics only
-65	3.33 V	0.258 V	3.07 V	489 μF	Ceramics only (final load test)
-66	2.80 V	—	—	—	Battery OCV below buck minimum (2.5V)
-67	2.30 V	—	—	—	Battery OCV collapse continues
-68	1.80 V	—	—	—	Battery OCV at STM32 minimum (1.8V)
-69	1.40 V	—	—	—	Battery OCV below single-cell nominal
-70	1.00 V	—	—	—	Battery effectively dead

The Key Insight: Effective Capacitance Calculation

The voltage drop during a constant-current pulse reveals which capacitors are doing the work:

$ C_{effective} = \frac{Q}{\Delta V} = \frac{I \times t}{\Delta V} = \frac{0.025A \times 0.060s}{\Delta V} = \frac{1.5 mC}{\Delta V} $

Effective Capacitance vs Temperature

This data tells the story perfectly:

At -55°C (C_eff = 18.75 mF): The effective capacitance is ~10× the combined capacitance of supercap + ceramic bank. This is impossible if capacitors were the only energy source—it proves the battery is still contributing current through the supercap’s low ESR. The supercap is functioning as intended, buffering battery current to meet the pulse demand.
At -56°C (C_eff = 2.63 mF): Effective capacitance has dropped to ~1.4× the nominal combined value. The supercap ESR is increasing, reducing its ability to pass battery current, but it’s still partially functional.
At -57°C (C_eff = 560 μF): The supercap has turned into a potato. The effective capacitance is now approximately equal to the ceramic bank alone (408 μF), with minor contribution from the supercap’s residual capacity. The ceramics have taken over completely.
From -58°C to -65°C (C_eff ≈ 430-490 μF): The effective capacitance stabilizes around the ceramic bank value. The slight excess over 408 μF comes from:
- Measurement uncertainty
- Residual supercap capacitance (it can still store charge, just can’t deliver current fast enough)
- ESR effects reducing apparent voltage drop efficiency

The handoff occurred exactly as predicted at -55°C to -56°C. The supercap’s ESR increase turns it from an energy buffer into a resistive barrier. The ceramics, with their temperature-stable solid dielectric, seamlessly take over pulse delivery.

Why Effective Capacitance Decreases Below -57°C

At -57°C and below, the effective capacitance should theoretically equal the ceramic bank (408 μF). But the measured values are slightly higher (430-490 μF). Why?

The ESR effect on voltage measurement:

When measuring Vmin under load, we measure at the end of the 60 ms pulse. During this time:

Ceramics immediately begin discharging (fast)
Battery attempts to trickle-charge through high-ESR supercap (slow)
The ESR causes a resistive voltage drop (V = IR), not a capacitive one (V = Q/C)

At extreme cold, the battery is still providing a tiny current through the frozen supercap:

At -60°C with R_supercap ≈ 45Ω and battery at 4.7V: $ I_{trickle} = \frac{V_{batt} - V_{cap}}{R_{supercap}} = \frac{4.7V - 3V}{45Ω} \approx 38 mA $

Wait—this is higher than our 25 mA load! But this calculation assumes the supercap voltage can drop to 3V. In reality, the battery’s internal resistance (16Ω at -60°C) limits current delivery:

$ I_{max} = \frac{V_{batt}}{R_{batt} + R_{supercap}} = \frac{4.7V}{16Ω + 45Ω} = 77 mA $

But this is the short-circuit current. Under our 25 mA load, the actual current from the battery through the supercap is:

$ I_{batt} = \frac{V_{batt} - V_{load}}{R_{batt} + R_{supercap}} $

At Vload = 1.23V (measured Vmin at -60°C): $ I_{batt} = \frac{4.7V - 1.23V}{16Ω + 45Ω} = \frac{3.47V}{61Ω} = 57 mA $

This exceeds the 25 mA load current! The battery is actually trying to charge the ceramics during the pulse. This explains why effective capacitance appears higher than 408 μF—the battery is supplementing the ceramic discharge.

The implication: Even at -60°C, the cascade architecture is partially working. The battery can’t supply the full load, but it’s contributing what it can through the high-ESR path. The ceramics handle the instantaneous demand while the battery backfills.

Critical Observations

-55°C represents the last “normal” operating point: 80 mV voltage sag under 25 mA load indicates the supercap is still functioning. Effective capacitance of 18.75 mF proves battery current is flowing freely through low supercap ESR.
-56°C to -57°C marks the supercap death: Effective capacitance drops from 2.63 mF to 560 μF—an 80% collapse. This is the supercap’s ESR transition point where it stops being a buffer and becomes a barrier.
Below -57°C, ceramics carry the load: Effective capacitance stabilizes at 430-490 μF, consistent with the 408 μF ceramic bank. The ceramics work exactly as specified.
Below -65°C, voltage collapse is the killer: Not capacitor failure, but battery OCV dropping below the buck converter’s 2.5V minimum (or the STM32’s 1.8V minimum for direct connection). No amount of capacitance can fix a voltage source that doesn’t have voltage.
High impedance vs low voltage: We can engineer around high impedance (trickle charging into capacitor banks). We cannot engineer around a voltage source that provides insufficient voltage. This is the surprise finding.

Energy Analysis: What the Capacitors Actually Deliver

The ceramic bank’s purpose is to provide short-duration pulse energy when the battery/supercap combination cannot deliver instantaneous current. Let’s analyze whether the bank fulfills this role:

Available Energy in Ceramic Bank (408 μF):

$ E = \frac{1}{2}CV^2 $

At -55°C (Vmax = 5.07V): $ E = \frac{1}{2}(408 \times 10^{-6})(5.07)^2 = 5.24 \text{ mJ} $

At -60°C (Vmax = 4.70V): $ E = \frac{1}{2}(408 \times 10^{-6})(4.70)^2 = 4.51 \text{ mJ} $

Required Energy for 25 mA × 60 ms pulse:

Assuming average voltage during pulse ≈ 3V (midpoint between start and end): $ E_{required} = 0.025 A \times 3V \times 0.060 s = 4.5 \text{ mJ} $

The ceramic bank alone cannot sustain the pulse. With only 4.5-5.2 mJ of stored energy and a requirement of 4.5 mJ, there’s essentially no margin.

Why the system fails below -57°C:

The ceramics deplete their stored charge within the first few milliseconds of the pulse. The remaining 50+ ms must be sustained by current flow from the battery through the supercapacitor. At temperatures below -57°C, the battery/supercap ESR is so high that this current flow causes catastrophic voltage collapse.

The ceramic bank provides initial voltage support (the first ~10 ms of stable voltage), but cannot sustain a 60 ms pulse without continuous current input from upstream components.

The Buck Converter Boundary

The TI buck converter specified for Stratosonde operates with a minimum input voltage of approximately 2.5V. This creates a hard system boundary:

System State Analysis:

Temperature	Vmin Under Load	Buck Status	System Status
-55°C	4.99 V	Operating	Functional
-56°C	4.27 V	Operating	Functional
-57°C	2.13 V	Below minimum	Brownout
-58°C to -65°C	<2.0 V	Below minimum	Failure
-66°C to -70°C	N/A (no load)	No load: 2.8V→1.0V	Battery depleted

The buck converter boundary at 2.5V creates a cliff effect:

At -56°C: System operates normally (Vmin = 4.27V, 1.77V margin)
At -57°C: System fails instantly (Vmin = 2.13V, 0.37V below minimum)

There is no graceful degradation across this boundary. The system transitions from “working” to “dead” within a 1°C temperature change.

Physical Interpretation: Why the Cliff?

The sharp transition between -56°C and -57°C demands physical explanation. Several compounding mechanisms contribute:

1. Electrolyte Phase Transition

Both the supercapacitor and LTO batteries use liquid electrolytes that become increasingly viscous as temperature drops. Near -57°C, the electrolyte approaches its glass transition temperature:

For typical organic electrolytes (EC:DMC):

Melting point of EC: 36°C
Melting point of DMC: 4°C
Eutectic mixture: ~-20°C to -30°C
Glass transition: approximately -55°C to -60°C

Below the glass transition, ionic conductivity doesn’t just decrease—it drops exponentially as the electrolyte transitions from a viscous liquid to an amorphous solid.

2. Lithium-Ion Mobility Collapse

The activation energy for lithium-ion transport increases sharply below -50°C:

$ \sigma = \sigma_0 \exp\left(-\frac{E_a}{kT}\right) $

Where:

σ = ionic conductivity
E_a = activation energy (~0.4-0.6 eV for LTO)
k = Boltzmann constant
T = absolute temperature

At -55°C (218 K) vs -57°C (216 K): $ \frac{\sigma_{-55}}{\sigma_{-57}} = \exp\left(\frac{E_a}{k}\left(\frac{1}{216} - \frac{1}{218}\right)\right) $

For E_a = 0.5 eV: $ \frac{\sigma_{-55}}{\sigma_{-57}} = \exp(0.5 \times 42.5) \approx 1.5\text{×} $

This 50% conductivity change over 2°C explains the transition cliff—small temperature differences cause large performance changes in this regime.

3. Charge Transfer Kinetics

At the electrode-electrolyte interface, the Butler-Volmer equation governs charge transfer:

$ i = i_0 \left[\exp\left(\frac{\alpha_a F \eta}{RT}\right) - \exp\left(-\frac{\alpha_c F \eta}{RT}\right)\right] $

The exchange current density i₀ is strongly temperature-dependent:

$ i_0 = i_0^{ref} \exp\left[-\frac{E_{act}}{R}\left(\frac{1}{T} - \frac{1}{T_{ref}}\right)\right] $

At -57°C, the exchange current density has dropped to approximately 0.1% of room temperature values, making the electrode-electrolyte interface a significant impedance contributor.

4. SEI Layer Resistance

The solid-electrolyte interphase (SEI) layer on battery electrodes normally presents minimal resistance. At extreme cold, the SEI becomes a thick resistive barrier:

Room temperature SEI resistance: ~1–5 Ω·cm²
-60°C SEI resistance: ~50-200 Ω·cm²

For the HTC1015’s small electrode area (~2 cm²), this contributes an additional 25-100Ω of resistance at extreme cold.

Comparison to Previous Characterizations

This test extends and validates the previous component-level characterizations:

LTO Battery (from Nov 23 post):

At -60°C: R_int = 8000 mΩ per cell = 16Ω for 2S
This test: Vmax = 4.70V at -60°C, consistent with 2S LTO at ~35% SOC

Supercapacitor (from Nov 24 post):

At -60°C: ESR = 45.4Ω, voltage collapse under 100 mA
This test: Combined with ceramics, 25 mA still causes collapse

Ceramic Capacitors (theoretical):

Expected: <50 mΩ ESR at -65°C
This test: Ceramics contribute negligible ESR; system failure due to battery/supercap

The data confirms that the cascading architecture reaches its fundamental limit not due to ceramic capacitor failure, but due to the upstream power sources (LTO + supercap) entering their catastrophic degradation regime.

Operational Implications

Usable Operating Range

Based on this characterization, the Stratosonde power system has the following operational envelope:

Temperature Range	Power Mode	Transmission Capability
+25°C to -40°C	Normal	Full power, all data fields
-40°C to -55°C	Degraded	Reduced power, supercap-buffered
-55°C to -56°C	Minimal	25 mA, 60 ms pulse only
-57°C to -65°C	Non-functional	Transmission causes brownout
Below -65°C	Dead	No-load voltage below 2.5V

The operational floor is -56°C, not the theoretical -60°C or -65°C assumed in previous analyses. Below -56°C, the system cannot transmit without browning out.

Mission Planning Impact

For stratospheric missions, this data constrains operational planning:

Standard Atmosphere at Float Altitude:

18 km: -56.5°C (at operational floor)
20 km: -56.5°C (at operational floor)
25 km: -51.5°C (within operating range)

At the standard stratospheric temperature of -56.5°C, the system operates precisely at its limit. Any temperature excursion colder than standard (due to polar vortex, seasonal variation, or altitude change) could push the system below the operational floor.

Thermal Management Becomes Critical:

The 1°C margin between -55°C (functional) and -57°C (failure) means that active thermal management is not optional—it’s mission-critical. The mylar enclosure and Zener heating strategy documented in previous posts must deliver at least 1-2°C of warming to ensure reliable operation at standard stratospheric temperature.

Minimum Viable Transmission

If the system operates at exactly -55°C (the last reliable point), the 25 mA/60 ms pulse represents the minimum viable transmission:

LoRaWAN Parameters:

SF7 (fastest spreading factor)
8 bytes payload (position + battery voltage only)
+14 dBm output power (reduced from +20 dBm)
60 ms airtime

Link Budget:

At +14 dBm output power with SF7:

Sensitivity: -124 dBm
Path loss at 30 km altitude to ground gateway: ~145 dB free space + 5 dB margin
Minimum path loss budget: 145 + 5 = 150 dB
Available link budget: +14 dBm - (-124 dBm) = 138 dB

This is insufficient for reliable communication.

At 30 km altitude (typical float), the reduced-power transmission has a 12 dB link margin deficit. This means:

Transmissions may be received by favorable gateways (urban areas with many receivers)
Transmissions will likely fail in areas with sparse gateway coverage
Signal may be received but not decoded (below sensitivity threshold)

Implication: The ceramic bank architecture enables transmission at extreme cold, but doesn’t guarantee successful communication. The reduced power level trades link margin for system survival.

Ceramic Bank Sizing: This Was a Validation Test

The 408 μF ceramic bank in this test was deliberately undersized. The goal was not to demonstrate a production-ready power system—it was to validate that:

Ceramic capacitors behave predictably at extreme cold (they do)
The supercap-to-ceramic handoff occurs as expected (it does, right at -55°C)
There are no unexpected failure modes in the ceramic layer (there aren’t)

The real ceramic requirement depends on the voltage floor:

To keep Vmin above the buck converter minimum (2.5V) or STM32/LoRa minimum (1.8V), we need:

$ C_{required} = \frac{I \times t}{\Delta V_{max}} $

For 25 mA × 60 ms with ΔV_max = 2.5V (from 5V to 2.5V): $ C_{required} = \frac{0.025 A \times 0.060 s}{2.5 V} = 600 \mu F $

For 25 mA × 60 ms with ΔV_max = 3.2V (from 5V to 1.8V direct to STM32): $ C_{required} = \frac{0.025 A \times 0.060 s}{3.2 V} = 469 \mu F $

The 408 μF bank is marginal even for the direct-to-STM32 case. The production design will need:

600-800 μF minimum for buck converter operation (2.5V floor)
500-600 μF for direct 1.8V STM32/LoRa operation (bypassing buck entirely at extreme cold)

This test validated the ceramics work—now we know how much we need.

Mass Impact:

Typical ceramic capacitors (C0G/NP0, 6.3V, 100 μF):

Package: 1210 or 1812
Mass: ~0.5g each
ESR: <50 mΩ

Production design (800 μF):

8× 100 μF capacitors
Mass: ~4g
Cost: ~$2-3

This is a trivial mass and cost penalty for enabling operation 15°C colder than battery-only designs.

The Unresolved Problem:

More ceramic capacitance solves the -57°C brownout issue. It does not solve the -65°C voltage collapse. Below -65°C, the battery OCV drops below 2.5V even at no load. No capacitor bank can fix a voltage source that provides insufficient voltage.

This is the fundamental limit. The cascade architecture (LTO → supercap → ceramic) extends operation from -40°C (battery only) to somewhere between -55°C and -65°C depending on thermal management. But electrochemistry imposes a hard floor.

Recommendations for Future Iterations

Hardware Modifications

Increase supercapacitor capacitance: The 1.5 mF supercap depletes too quickly. A 5-10 mF supercap would provide longer pulse sustaining capability, though at the cost of slower charging current from the battery.
Consider alternative electrolytes: Some supercapacitors use low-temperature electrolytes (e.g., acetonitrile-based) that maintain lower ESR to -65°C. This could shift the cliff point colder by 5-10°C.
Investigate ceramic supercapacitors: Emerging ceramic dielectric supercapacitors combine the temperature stability of ceramics with higher capacitance. A 100 μF ceramic supercap could provide both buffer capacity and temperature stability.

Firmware Modifications

Temperature-aware power management: Firmware should monitor battery temperature and disable transmission attempts below -55°C. Attempting transmission below this threshold wastes energy and accomplishes nothing.
Adaptive pulse duration: At -55°C, even a 40 ms pulse instead of 60 ms would reduce energy requirements by 33%, potentially extending the operational floor by 1-2°C.
Burst transmission scheduling: Rather than transmitting every 5 minutes, accumulate data and transmit in bursts when temperature rises (during thermal transients from balloon rotation or altitude changes).

Thermal Management Enhancement

Prioritize battery heating over supercapacitor: The LTO cells are the limiting factor. Any available heating should target the batteries first.
Exploit altitude oscillations: Float altitude naturally oscillates ±500-1000m. Schedule transmissions for altitude peaks (where temperature is slightly warmer) rather than troughs.
Consider sun-synchronous rotation: If the payload can be designed to rotate slowly, one side will always face the sun, providing continuous solar heating.

Conclusion: Validation Complete, Surprise Discovered

This test set out to confirm that ceramic capacitors would seamlessly take over when the supercapacitor fails at extreme cold. That prediction was validated perfectly. The effective capacitance calculations show the handoff occurring exactly as expected:

What We Expected	What We Measured
Supercap works until ~-55°C	C_eff = 18.75 mF at -55°C (supercap + battery contributing)
Supercap fails below -55°C	C_eff drops to 560 μF at -57°C (ceramics only)
Ceramics work at all temperatures	C_eff stable at 430-490 μF from -57°C to -65°C

The ceramics performed exactly as their specifications promised. Class I (C0G/NP0) dielectrics are temperature-stable because they’re solid—no electrolyte to freeze, no ion mobility to collapse. The cascade strategy is validated.

The Surprise: Battery Voltage Collapse Below -65°C

We expected high impedance. We can engineer around high impedance—the cascade architecture accumulates energy via trickle charging, building up charge in capacitors over time regardless of how slowly current flows.

We did not expect the battery open-circuit voltage to collapse to unusable levels. Below -65°C:

-66°C: Vmax = 2.8V (barely above buck minimum)
-67°C: Vmax = 2.3V (below buck minimum)
-68°C: Vmax = 1.8V (at STM32/LoRa minimum)
-70°C: Vmax = 1.0V (essentially zero)

This is not an impedance problem—it’s a thermodynamic problem. The electrochemical potential of the LTO cell decreases as temperature drops. At -70°C, the lithium-ion insertion/extraction reaction approaches its thermodynamic limit.

You cannot charge a capacitor from a voltage source that provides no voltage.

This sets the absolute floor for the cascade architecture at approximately -65°C, independent of capacitor sizing, thermal management, or any other engineering mitigation.

Next Steps:

Increase ceramic bank to 600-800 μF to maintain Vmin > 2.5V during transmission (straightforward)
Focus thermal management on keeping batteries above -55°C (the supercap-to-ceramic transition point)
Accept -65°C as a hard electrochemical limit—no engineering can overcome a battery that produces insufficient voltage

The cascading power architecture works. The ceramics are validated. The fundamental limit is now known: it’s not capacitor failure, it’s battery voltage collapse. Design accordingly.

Test configuration: 2S HTC1015 LTO cells in series, 1.5mF supercapacitor (5.5V) in parallel, 408μF ceramic capacitor bank in parallel. Load: 25mA for 60ms. No load applied below -65°C due to battery voltage below buck converter minimum (2.5V).

Raw characterization data: ceramic_bank_test.csv